python版DTW动态时间规划算法

2022 年 10 月
一	二	三	四	五	六	日
	1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30
31

前言

最近遇到一个问题，就是计算三维空间上两条曲线（一系列的点（x,y,z））相似度。

最开始使用 豪斯多夫(Hausdorff)距离可以简易计算出，两条曲线之间的距离。

但是hausdorff有明显的两个BUG：

1）就是不支持回程。比如一个 “V”t型的曲线，

2）两条曲线长度不一致。比如：line1='---^--v---', line2='-----------^------v-'，其实两条曲线相似度应该很高的，但是hausdorff算出来就很低。

为了解决这个问题，网上查了很多资料，提出，使用hausdorff+时间(t)，来解决回程问题，但是后面我搜索到了DTW算法，这个算法主要用于语音波形图识别。和我的需求很相似。于是就试了一下，感觉还可以。

后面又找到了专注轨迹相似度算法LCSS。下篇文章试试这个算法的效果，今天我们主要聊DTW。

概述

DTW （Dynamic time warping）算法是可以度量两个独立时间序列的相似度的一种方法。曾被广泛应用在单词音频的匹配上。该方法主要用来解决在两段序列的时长不同的情况下，进行相似度的判断。
例子1
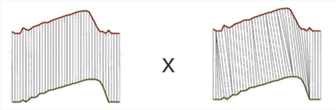
上图中，左侧时长相等，可以逐一进行欧式距离的计算，右侧则是时长不等，经过DTW之后得到的结果，可以看出来两个序列并不是一一对应的。
例子2
再比如上面左图，要得到蓝色序列与红色序列的相似度，因为可以看出来两个序列有经过平移的迹象，直接用一一匹配的方法显然是不合理的。要得到左图的对应效果，就需要用DTW方法。

CODE:

import numpy as np
import math
line1 =[
{'x':0,'y':0,'z':0},
{'x':1,'y':0,'z':0},
{'x':2,'y':0,'z':0},
{'x':3,'y':0,'z':0},
{'x':4,'y':0,'z':0},
{'x':5,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':8,'y':0,'z':0},
{'x':9,'y':0,'z':0},
{'x':8,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':6,'y':0,'z':0}
]
line2 =[
{'x':0,'y':0,'z':0},
{'x':1,'y':0,'z':0},
{'x':2,'y':0,'z':0},
{'x':3,'y':0,'z':0},
{'x':4,'y':0,'z':0},
{'x':5,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':7,'y':0,'z':0},
{'x':8,'y':0,'z':0},
{'x':10,'y':0,'z':0},
{'x':8,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':6,'y':0,'z':0},
{'x':5,'y':0,'z':0},
{'x':4,'y':0,'z':0}
]
def get_distance(a, b):
return math.dist([a['x'], a['y'], a['z']],[b['x'],b['y'],b['z']])
pass
print('line1:'+str(len(line1)))
print('line2:'+str(len(line2)))
result = np.full((len(line1)+1, len(line2)+1), np.inf)
result[0,0]=0
for i in range(1, len(line1)):
for j in range(1, len(line2)):
a = line1[i]
b = line2[j]
result[i+1, j+1]= get_distance(a, b)
for i in range(1, len(line1)):
for j in range(1, len(line2)):
a = line1[i]
b = line2[j]
result[i,j ]= get_distance(a, b)+ min(result[i-1][j], result[i][j-1], result[i-1][j-1])
print('---------------DTW-----------------')
print(result)
print('---------------Distance----')
print((result[len(line1)-1, len(line2)-1]))
print(len(a)+len(b))
print(result[len(line1)-1, len(line2)-1]/(len(a)+len(b)))

大佬总结的计算两条曲线相似度的算法：

基于点方法： EDR，LCSS，DTW等。

基于形状的方法： Frechet， Hausdorff

基于分段的方法：One Way Distance, LIP distance

基于特定任务的方法：TRACLUS， Road Network，grid等

注：

LCSS最长公共子序列算法，常用于轨迹相似度算法，这个更适合？

EDR编辑距离算法，常用于字符串相似度算法。

原文：https://www.zhihu.com/question/27213170

链接

近期文章

热门标签

新人福利，免费薅羊毛

前言

概述

CODE:

大佬总结的计算两条曲线相似度的算法：

============ 欢迎各位老板打赏~ ===========

与本文相关的文章

发表评论